This post is going to cover a simple, easy and fast method to calculate the load take down in a structure. A heads up, this is an approximation and should NOT be used for detailed design.

All assumptions should err on the side of caution or be conservative.

What is Load Take Down?

So, what is load take down? This is the load that we expect to see in the foundations. The reactions in structure. The roof and every floor will have force acting upon it, we need to assess how the load goes from each floor to the ground. It can then be safely distrubed into the ground via the foundations.

Structures can be quite complicated and without exploring the detailed design we need to make assumptions.

Why Estimate Foundation Loads?

Estimating foundation loads during the initial design scheme is very important. It allows us to decide what type of foundation solutions that we can use, makes us aware of any potential issues with the ground and if ground strengthening works will be required. It also allows us to quickly assess the overall cost of each solution. In some cases it may be seen that it is not viable or cost efficient to build a structure and in this case, we should get in touch with the developer or client and let them know. We might lose a business on this one project but overall the client will be thankful and will be much more likely to come back to us in the future for business.

When we estimate the foundation loads we can also use the results to check and validate our structural model. The loads will not be exact but we should be able to gauge if it is in the right ballpark.

A rule of thumb we have at our company is that all engineers should complete a load take down assessment before proceeding with the detailed design.

In various places I have been little mistakes that have been made during the modelling process that were not picked up.

Our Assumptions for Calculating the Foundation Loads

Below is a list of assumptions we can use to simplify the calculations.

• We will only use the most critical loaded widths
• We will only use the most critical spans
• The structure is braced and will transfer all lateral loads.
• The wind load calculation will be done separately, bracing will provide uplift affecting the foundation solution.
• We will make a reference to a national annex or the codes of practise to estimate the loads.
• We have to assume the floor construction. We will make this uniform throughout the whole structure.

Feel free to add additional assumptions to increase the accuracy of the results. Personally, I wouldn’t do any less. Ignoring the bracing forces may cause issues with potential foundation schemes going forward, normally I do a separate check to look at the bracing forces (shear and uplift).

Write down all your assumptions and loads you have used and attach it to the calculations. Typically, we could do an exercise like this and then not revisit the project for days or even weeks.

Load Transfer Through a Structure

Before going into a worked example, we will look at individual elements or members that will transfer load and look globally at the whole structure.

From the diagram below, we can see a one way slab. The load spans between the beams and is then transferred to the columns.

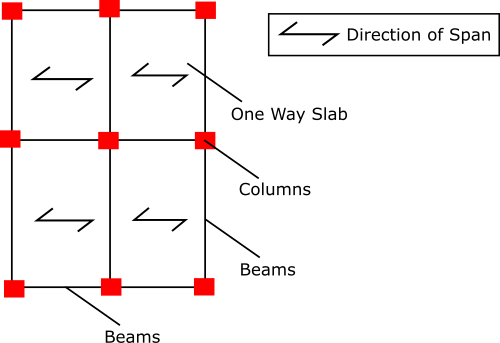
Once the load gets to the columns from the beam, it is transferred down the columns into the foundations. The load on the foundations is exactly what we want to calculate.

Remember, load goes from the beams, to the column and finally to the foundations. Load always needs to go into the ground to be dissipated.

The example below is a simple, it assumes a single story with just one type of load acting on the beams. We want to try and imagine every structure to be like the one below as this allows us to estimate the loads on the foundations in only a few lines of calculations.

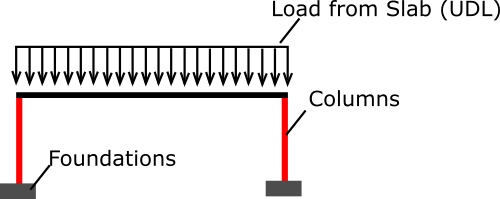
Normally, we would have permanent loads (dead loads) and imposed loads (live loads). It is up to you if you choose to factor the dead and live loads in accordance with the local standards/codes of practise.

When I am accessing the load take down, if we are going to assume a piled solution due to poor ground, I leave the loads unfactored. This is because pile contractors/suppliers normally state a safe working load (SWL) which has already been factored. For ground bearing solutions such as pad foundations, I would factor the loads.

Calculating Column Reactions

We will run through how to calculate the column reactions, using the above example, our aim is to find the most critical axial force that is to be transferred into the foundations.

Below we have beams that span 8m and slabs that span 6m. We have also been provided the dead and live loads, 1kN/m² and 5kN/m² respectively.

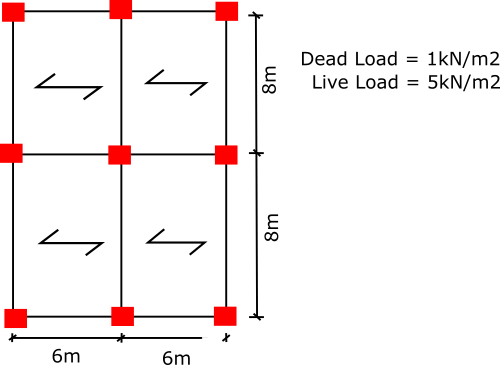
We need to convert the area loads to a uniformly distributed load (UDL) that acts on the beam. The grey area shows the load influence that acts on the beam, half of each slab that spans onto it. Therefore the total slab load that will act upon the beam will be 3m + 3m (6m).

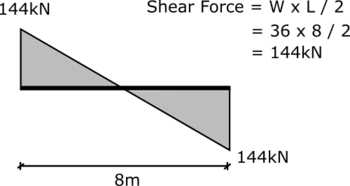
So, we have a UDL acting on the beam, using simple beam formulas, we can calculate the shear force acting at the supports. The supports are the columns. For the analysis, we will add up both the dead and live load as we will not factor them separately.

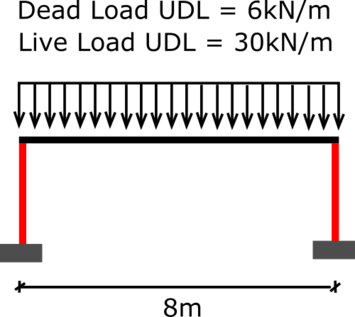
Calculating the shear force in the beam.

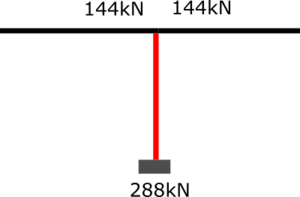
Since we only have one storey to consider in this example, the 144kN load will be the force that is directly transferred from the beam to the column. Looking at the elevation below we can see that one column supports two beams. Therefore 288kN will be transferred from the beam to the column.

Worked Example - 3 Storey Office Block

We will now look at a full example, we will only calculate the loads on the most critical column/foundation.

It is a three storey office block, all the loads have been provided. We will ignore all wind loads acting on the structure.

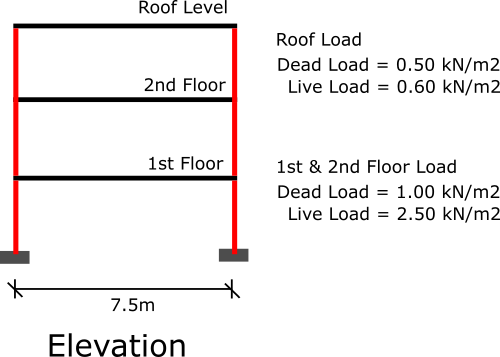
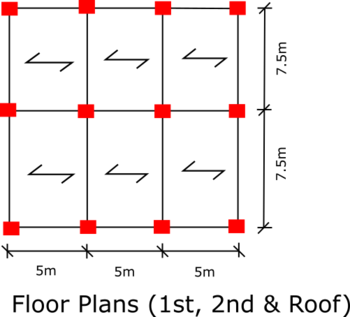
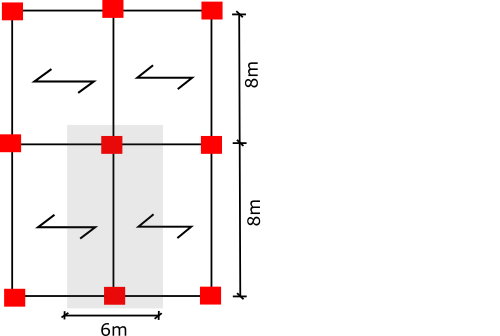
To begin, we need to find the most critical column in the whole structure. In this example it can be one of many columns in the centre of the structure. Below, a column we will use is highlighted in grey.

As we have different loads for the roof and the other floors, we need to find out the loads for each floor. We will work through the roof and the floors then calculate the loads getting transferred into the column.

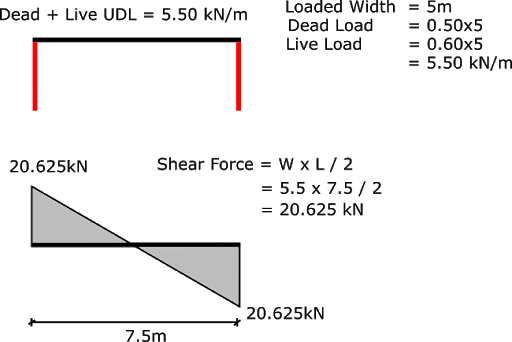
Roof Loads..

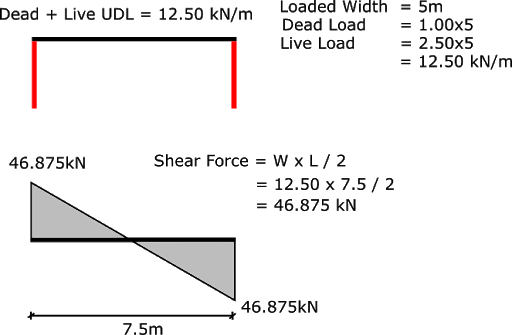
Floor Loads..

Now we need to add up all the column reactions to find out the force that will go into the foundations.

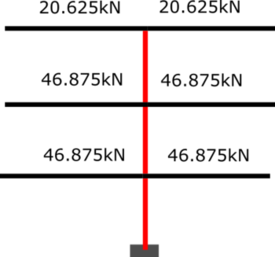
Total force going into the foundations = 228.75kN